Introduzione al Teorema di Bayes
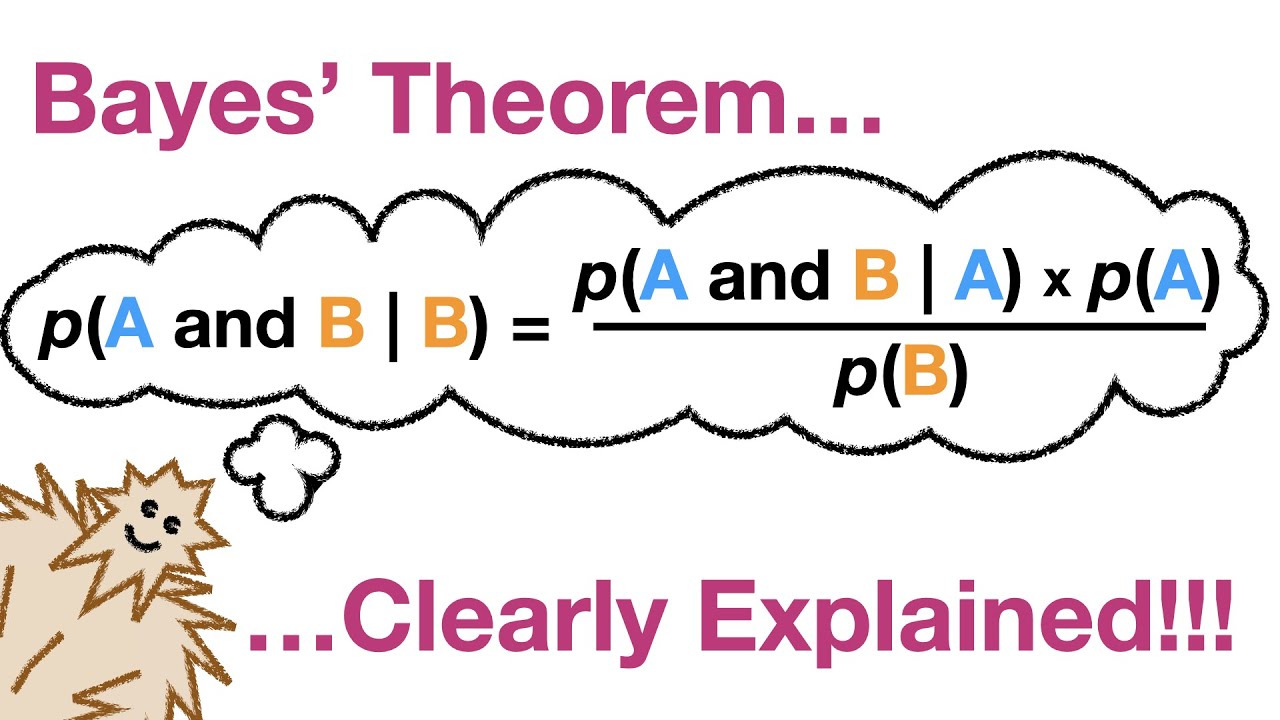
Il teorema di Bayes è un potente strumento matematico utilizzato per aggiornare le probabilità di un evento sulla base di nuove informazioni. Questo teorema è fondamentale in diversi campi, tra cui la statistica, l’intelligenza artificiale e la medicina, dove viene applicato per prendere decisioni basate su dati incerti.
Probabilità Condizionata e Teorema di Bayes
La probabilità condizionata è la probabilità che un evento si verifichi dato che un altro evento si è già verificato. Il teorema di Bayes fornisce un modo per calcolare la probabilità condizionata di un evento, in particolare quando si dispone di informazioni a priori sull’evento e di nuove informazioni che possono influenzare la probabilità.
Componenti del Teorema di Bayes
Il teorema di Bayes è composto da quattro componenti principali:
- Probabilità a priori (P(A)): la probabilità di un evento A prima di osservare nuove informazioni.
- Probabilità a posteriori (P(A|B)): la probabilità di un evento A dopo aver osservato nuove informazioni B.
- Probabilità di verosimiglianza (P(B|A)): la probabilità di osservare le nuove informazioni B dato che l’evento A si è verificato.
- Probabilità marginale (P(B)): la probabilità di osservare le nuove informazioni B, indipendentemente dall’evento A.
Il teorema di Bayes può essere espresso dalla seguente formula:
P(A|B) = [P(B|A) * P(A)] / P(B)
Esempio Pratico, Bayesian
Immaginiamo di voler diagnosticare una malattia. Sappiamo che la malattia è rara, con una probabilità a priori del 1%. Un nuovo test diagnostico è disponibile, con una probabilità di verosimiglianza del 90% di risultare positivo se la persona è malata e una probabilità di verosimiglianza del 5% di risultare positivo se la persona è sana.
Se una persona fa il test e risulta positivo, qual è la probabilità che sia effettivamente malata?
Possiamo usare il teorema di Bayes per calcolare la probabilità a posteriori:
P(Malato|Positivo) = [P(Positivo|Malato) * P(Malato)] / P(Positivo)
Sapendo che P(Positivo|Malato) = 0.9, P(Malato) = 0.01 e P(Positivo) = (0.9 * 0.01) + (0.05 * 0.99) = 0.0585, possiamo calcolare:
P(Malato|Positivo) = (0.9 * 0.01) / 0.0585 = 0.154
Quindi, la probabilità che una persona sia effettivamente malata dato che il test è positivo è del 15.4%.
Applicazioni del Teorema di Bayes: Bayesian

Il Teorema di Bayes, pur essendo un concetto matematico relativamente semplice, trova un’ampia gamma di applicazioni in diversi campi, dalla scienza alla medicina, dall’informatica all’economia. Questo teorema è fondamentale per l’analisi di probabilità condizionate, ovvero la probabilità di un evento dato che un altro evento si è già verificato.
Inferenza Statistica
L’inferenza statistica si basa sull’utilizzo di dati campionari per trarre conclusioni su una popolazione più ampia. Il teorema di Bayes è fondamentale in questo contesto, poiché consente di aggiornare le nostre convinzioni sulla probabilità di un evento alla luce di nuove evidenze.
Ad esempio, in un test clinico per un nuovo farmaco, possiamo utilizzare il teorema di Bayes per calcolare la probabilità che un paziente abbia una determinata malattia, dato che il test è risultato positivo. Il teorema di Bayes ci permette di considerare la probabilità a priori della malattia nella popolazione, la sensibilità e la specificità del test, e la probabilità di un risultato positivo del test.
Classificazione
La classificazione è il processo di assegnazione di elementi a categorie predefinite. Il teorema di Bayes è utilizzato in molti algoritmi di classificazione, come il classificatore Bayesiano Naïve. Questo algoritmo assume che le caratteristiche di un elemento siano indipendenti tra loro, il che semplifica il calcolo delle probabilità.
Un esempio di applicazione è il filtro antispam, che utilizza il teorema di Bayes per classificare le email come spam o non spam. Il filtro analizza le parole presenti nell’email e le confronta con un database di parole associate allo spam. Utilizzando il teorema di Bayes, il filtro calcola la probabilità che un’email sia spam, dato il contenuto delle parole.
Riconoscimento di Pattern
Il riconoscimento di pattern è il processo di identificazione di modelli o schemi in dati complessi. Il teorema di Bayes è utilizzato in algoritmi di riconoscimento di pattern, come le reti bayesiane, che sono modelli grafici che rappresentano le relazioni di dipendenza tra variabili.
Un esempio di applicazione è il riconoscimento vocale, che utilizza il teorema di Bayes per identificare le parole pronunciate da un utente. Il sistema analizza i segnali acustici e li confronta con un database di parole, utilizzando il teorema di Bayes per calcolare la probabilità che ogni parola sia stata pronunciata.
Analisi dei Dati
Il teorema di Bayes è uno strumento fondamentale per l’analisi dei dati, poiché consente di aggiornare le nostre convinzioni sulla probabilità di un evento alla luce di nuovi dati. Ad esempio, in un’analisi di mercato, possiamo utilizzare il teorema di Bayes per calcolare la probabilità che un prodotto abbia successo, dato il numero di vendite nei primi mesi.
Medicina
Il teorema di Bayes ha un’ampia gamma di applicazioni in medicina, come la diagnosi di malattie, la valutazione dei rischi e la previsione dell’esito di un trattamento. Ad esempio, in un test di screening per il cancro, il teorema di Bayes può essere utilizzato per calcolare la probabilità che un paziente abbia il cancro, dato che il test è risultato positivo.
| Campo | Applicazione | Esempio |
|---|---|---|
| Inferenza Statistica | Calcolo della probabilità di un evento dato che un altro evento si è già verificato | Calcolo della probabilità che un paziente abbia una determinata malattia, dato che il test è risultato positivo. |
| Classificazione | Assegnazione di elementi a categorie predefinite | Filtro antispam che utilizza il teorema di Bayes per classificare le email come spam o non spam. |
| Riconoscimento di Pattern | Identificazione di modelli o schemi in dati complessi | Riconoscimento vocale che utilizza il teorema di Bayes per identificare le parole pronunciate da un utente. |
| Analisi dei Dati | Aggiornamento delle convinzioni sulla probabilità di un evento alla luce di nuovi dati | Calcolo della probabilità che un prodotto abbia successo, dato il numero di vendite nei primi mesi. |
| Medicina | Diagnosi di malattie, valutazione dei rischi e previsione dell’esito di un trattamento | Calcolo della probabilità che un paziente abbia il cancro, dato che il test è risultato positivo. |
Metodi e Tecniche Bayesiane

L’approccio bayesiano offre una serie di metodi e tecniche per l’analisi dei dati, consentendo di integrare la conoscenza pregressa con i dati osservati per ottenere inferenze più precise e informate. Questi metodi si basano sul teorema di Bayes, che fornisce una formula per aggiornare le credenze sulla base di nuove evidenze.
Inferenza Bayesiana
L’inferenza bayesiana è il processo di aggiornamento delle credenze su un parametro o un’ipotesi basandosi su nuovi dati. Questo processo si basa sul teorema di Bayes, che fornisce una formula per calcolare la probabilità a posteriori di un evento, data la probabilità a priori e la probabilità condizionata. L’inferenza bayesiana è un metodo potente per l’analisi dei dati perché consente di incorporare la conoscenza pregressa nel processo decisionale.
La probabilità a posteriori di un evento è proporzionale alla probabilità a priori dell’evento moltiplicata per la probabilità condizionata dell’evento dato i dati osservati.
Modello Bayesiano Lineare
Il modello bayesiano lineare è un’estensione del modello di regressione lineare che incorpora un’interpretazione bayesiana dei parametri. In questo modello, i parametri sono considerati variabili casuali con una distribuzione a priori. I dati osservati vengono utilizzati per aggiornare la distribuzione a priori dei parametri, ottenendo una distribuzione a posteriori. Il modello bayesiano lineare consente di ottenere stime più precise dei parametri e di valutare l’incertezza associata a queste stime.
Reti Bayesiane
Le reti bayesiane sono modelli grafici che rappresentano le relazioni di dipendenza tra variabili casuali. Queste reti sono costituite da nodi, che rappresentano le variabili, e da archi, che rappresentano le relazioni di dipendenza. Le reti bayesiane possono essere utilizzate per inferire la probabilità di un evento dato le evidenze osservate.
Le reti bayesiane sono modelli grafici che rappresentano le relazioni di dipendenza tra variabili casuali.
Tecniche di Apprendimento Bayesiano
Le tecniche di apprendimento bayesiano sono un insieme di algoritmi che utilizzano il teorema di Bayes per apprendere dai dati. Questi algoritmi utilizzano una distribuzione a priori per i parametri del modello e aggiornano questa distribuzione utilizzando i dati osservati. Le tecniche di apprendimento bayesiano sono utilizzate in una varietà di applicazioni, tra cui il riconoscimento di pattern, la classificazione e la previsione.
Le tecniche di apprendimento bayesiano sono un insieme di algoritmi che utilizzano il teorema di Bayes per apprendere dai dati.
Bayesian analysis, with its focus on updating beliefs based on evidence, offers a powerful framework for decision-making in various domains. This approach is particularly relevant in the world of luxury yacht construction, where companies like Perini Navi must constantly adapt to evolving customer preferences and market trends.
By leveraging Bayesian methods, such companies can refine their design and production processes, ultimately leading to more informed and successful outcomes.
Bayesian statistics, with its emphasis on updating beliefs based on evidence, can be applied to a variety of fields, including business and finance. For instance, understanding the dynamics of a successful entrepreneur like Mike Lynch, and his wife’s potential role in his ventures, mike lynch wife , can provide valuable insights into the interplay of personal and professional factors.
Applying Bayesian principles to analyze such case studies can help refine our understanding of how individuals and their relationships influence success in various domains.
